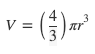As part of the SAT test, you will be expected to complete the SAT mathematics section alongside critical reading and writing.
The math portion of the SAT examination is intended to take the concepts you have learned in high school and apply them in new, and usually uncommon, ways. While this can be intimidating for students that are not well-versed in mathematics, if you allocate focus towards the fundamental math formulas and concepts included in the SAT exam - the score you receive will improve substantially.
Provided that you will provide attention to understanding the basis of math formulas and principles, what are the formulas that you will need to have committed to memory for the SAT math section on the day of your examination?
But before you get into this reading, get equipped with the acceptance rates of the top 100 selective colleges in yesterday's blog.
And if you are looking to participate in some high school competitions to make your college application stand out, here is a list of the best STEM contests 🧬 and a list of the uppermost competitive writing competitions. ✏️
Today's blog post will provide you with the list of important mathematical theorems and concepts that you absolutely must know before taking the SAT test. By understanding the list of formulas in this article, you will not only gain extra time for other sections of the SAT college entrance test but also increase the likelihood of getting a couple more questions correct on the exam. Here, we will give a list of formulas given on SAT Math.
For more information on an upcoming
UC Berkeley AI Program
that 7EDU is partnering up with, see the flyer at the end of this article!
The Exact Formulas Given on the SAT Examination
For starters, here is exactly what you should expect to see at the beginning of both of your SAT mathematics sections. Bookmark or download the image so that you can begin getting acquaint yourself with the formulas.
The total number of formulas provided to you during the SAT college admissions exam will be the 12 that you see on the image above, alongside three geometry laws. While it is most definitely useful (and time-efficient) to memorize the formulas and laws, it is not critical as they are offered on every part of the SAT math section.
High school students taking the SAT exam are given only geometrical formulas, so be sure to set your priorities in studying and memorizing your algebra and trigonometry theorems before the SAT exam date.
Note that after the new SAT exam was formulated, geometry now makes up less than ten percent of the math questions on the test. It was minimized from the examination so it is recommended that high school students place their study endeavors towards algebra.
While it can be easy to assume, "Oh so that means I don't need to know what the geometry formulas are/mean." This is not the case. You will need to nevertheless understand the geometrical concepts and theorems moving forward since the SAT math testing section remains with a handful of questions that you will need to complete.
As such, what do each of the formulas mean? 7EDU has got you covered. In an upcoming blog article, tune in for a comprehensive list of formulas not provided on the SAT math exam that you will need to know (so be sure to subscribe to our newsletter to be the latest to find out)!
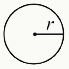
Area of a Circle
π can be written as 3.14 (or 3.14159)
r is the radius of the circle (any line segment from the center point of the circle, straight to the edge of the circle)
Circumference of a Circle
d is the diameter of the circle (any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It is also twice the radius.)
Area of a Rectangle
l is the length of the rectangle
w is the width of the rectangle
Area of a Triangle
b is the length of the base of the triangle
h is the length of the height of the triangle
In a right triangle, the height is the same as the side of the 90-degree angle
For those that are not right triangles, the height will be straight down from the interior of the triangle
The Pythagorean Theorem
In a right triangle, the two smaller sides of the triangle (a and b) are each squared (their sum will equal to the square of the hypotenuse c, the longest side of the triangle).
Properties of Special Right Triangle: Isosceles Triangle
Isosceles triangles have two sides that are equal in length as well as two equal angles opposite of those sides
Isosceles right triangles always have a 90-degree angle and two 45-degree angles
The side lengths are determined by s, s, s√2 where the hypotenuse (the side opposite of the 90-degree) having a length of one of the smaller sides *√2
For example, an isosceles right triangle may have the side lengths of 5, 5, 5√2
Properties of Special Right Triangle: 30, 60, 90 Degree Triangle
The side lengths are determined by the formula x, x√3, and 2x
The side opposite of the 30-degree angle is the smallest, with a measurement of x
The side opposite of the 60-degree angle is the middle length, with a measurement of x√3
The side opposite of the 90-degree angle is the hypotenuse (the longest side of the triangle), with a length of 2x
For example, a 30-60-90 triangle may have side lengths of 5, 5√3, and 10
Volume of a Rectangular Solid
l is the length of one of the rectangle's side
w is the width of one of the rectangle's side
h is the height of the rectangular figure
Volume of a Cylinder
r is the radius of the circular side of the cylinder
h is the height of the cylinder figure
Volume of a Sphere
r is the radius of the sphere
Volume of a Cone
r is the radius of the circular side of the cone
h is the height of the cone (measured from the center of the circular side to the pointed tip of the cone)
Volume of a Pyramid
l is the length of one of the edges of the rectangular side of the pyramid
h is the height of the pyramid figure at its peak (measured from the center of the rectangular side of the pyramid to the peak)
w is the width of one of the edges of the rectangular side of the pyramid